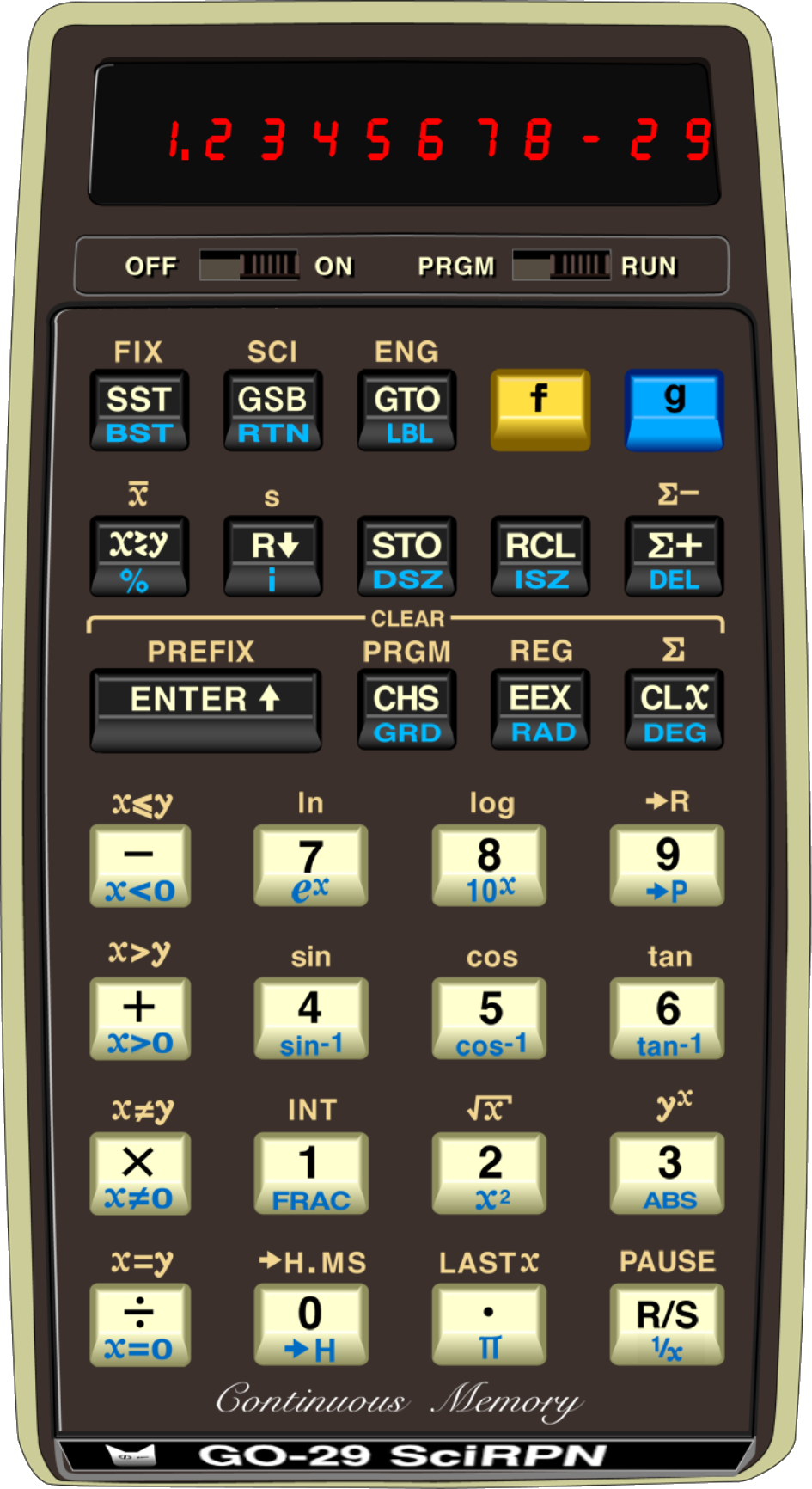
GO-29 SciRPN closely simulates the venerable HP-29C Programmable Pocket Scientific Calculator. The HP-29C was released in 1977 and sold for a MSRP of $195. Virtually indistinguishable from the real item in operation, GO-29 is a powerful yet simple retro calculator.
Copyright (©) 2019 - 2024 BigCatOS. All rights reserved. | Contact